자료구조   알고리즘   그래프   DFS   BFS

그래프 자료 구조와 BFS, DFS 알고리즘

February 27, 2021

summary

그래프 자료 구조를 이해하고, DFS, BFS 알고리즘을 작성한다.

그래프 자료 구조

노드간의 연결을 표현한 데이터 구조

그래프는 노드(점)와 엣지(선)로 이루어져 있다. 노드와 노드의 관계를 엣지로 표햔하며, 관계가 맺어져 있으면(연결돼 있으면) 해당 노드는 인접해 있다고 표현한다.

엣지에 방향 유무에 따라 유향, 무향그래프로 나뉜다. 엣지에 가중치가 부여되어 있으면 가중치 그래프라고 한다.

그래프 클래스 구현

그래프 클래스를 구현헤 보자. 그래프의 구현은 인접 행렬, 인접 리스트 등으로 구현할 수 있는데, 여기서는 인접 리스트 방식으로 구현한다. (각 노드는 인접한 노드 리스트를 가지고 있다)

Node 클래스 구현

먼저 그래프의 각 노드 클래스를 정의한다.

class Node {
  constructor(data) {
    this.data = data;
    this.adjacent = new Set();
  }

  link(linkTargetData) {
    this.adjacent.add(linkTargetData);
  }

  getAdjacent() {
    return [...this.adjacent.values()];
  }
}

생성자에서 데이터를 설정하고, 인접 노드를 표현하는 adjacent 를 집합으로 초기화한다.

Graph 클래스 뼈대 구현

그래프 클래스는 private 멤벼 변수로 nodes 를 갖는다. nodes 는 딕셔너리로, key 에 해당하는 값은 유일하다.

class Graph {
  #nodes = new Map();
}

노드 추가, 엣지 추가 구현

노드를 추가하는 메소드는 다음과 같이 구현한다. data 로 노드를 생성하고, data 를 key 로 nodes 딕셔너리에 값을 저장한다.

addNode(data) {
    const node = new Node(data);
    this.#nodes.set(data, node);
}

노드와 노드사이의 엣지는 아래와 같이 구현한다.

addEdge(v, w) {
    const firstNode = this.#nodes.get(v);
    const secondNode = this.#nodes.get(w);
    firstNode.link(secondNode.data);
    secondNode.link(firstNode.data);
}

nodes 에서 각각 값을 찾고, 해당 노드의 인접리스트에 상대 노드를 추가한다. Node 클래스의 link 메소드가 내부의 adjacentList 집합에 값을 추가한다.

helper method 추가

그래프의 내용을 확인하기 위해 그래프 안의 각 노드별로 해당 노드가 가진 인접 노드 리스트를 표시하는 print 메소드를 추가한다.

printGraphInfo() {
    this.#nodes.forEach((node) => {
      const { data, adjacent } = node;
      console.log(`${data}'s adjacent list: [${[...adjacent.values()].join(', ')}]`);
    });
}

그래프가 제대로 생성되는지 테스트 해 보자. 테스트를 위해 생성할 그래프의 모양은 아래와 같다.

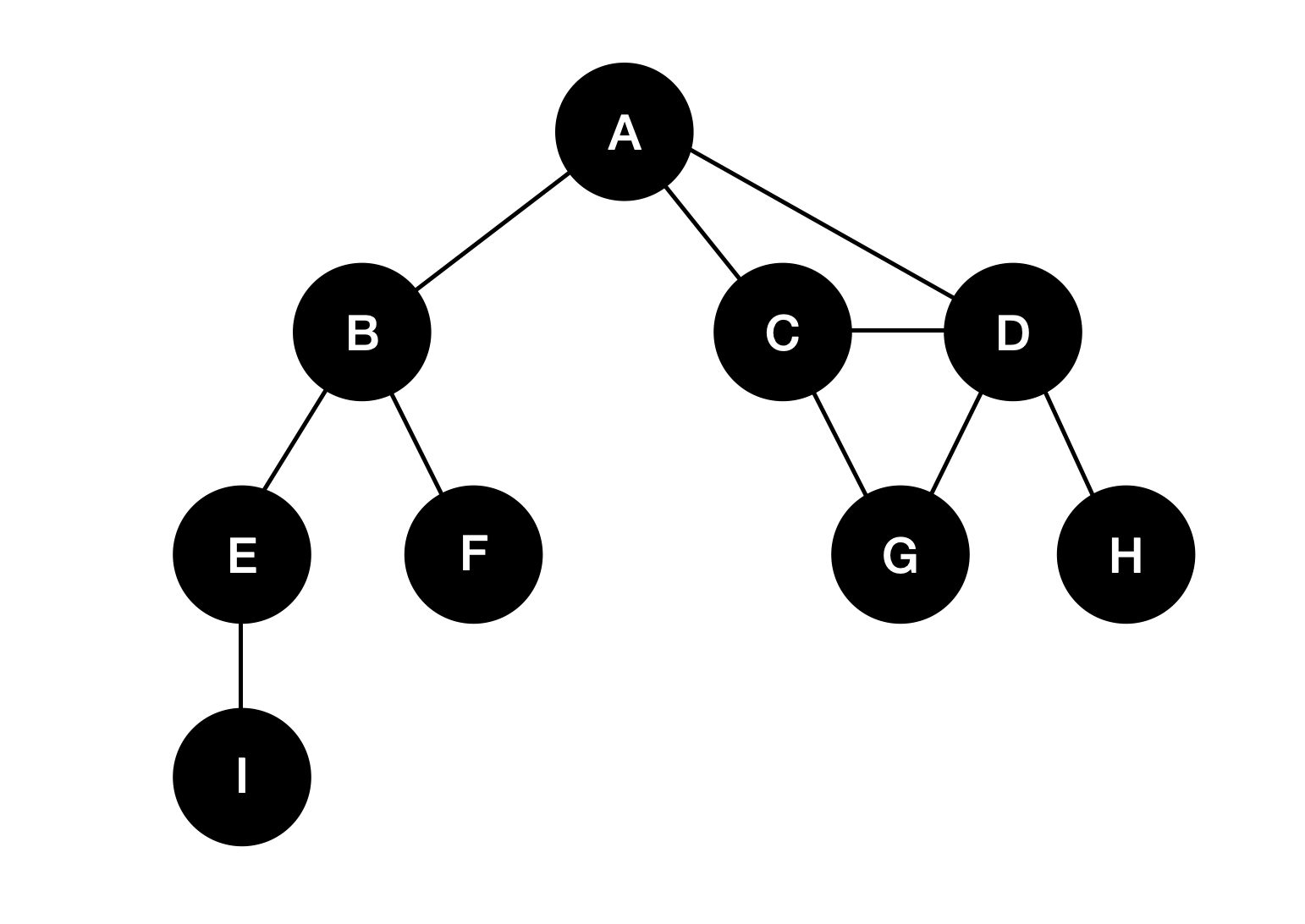
const graph = new Graph();
graph.addNode('A');
graph.addNode('B');
graph.addNode('C');
graph.addNode('D');
graph.addNode('E');
graph.addNode('F');
graph.addNode('G');
graph.addNode('H');
graph.addNode('I');

graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');

graph.printGraphInfo();

테스트의 결과는 다음과 같다.

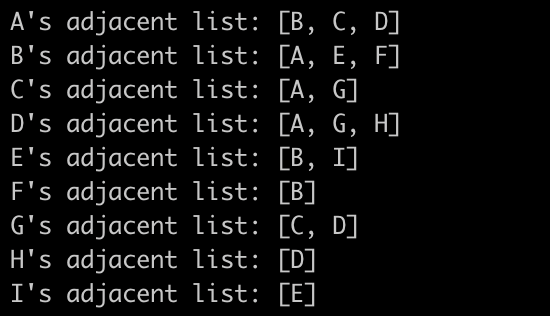
그래프의 탐색

그래프의 탐색은 방법에 따라 아래로 내려가면서 탐색하는 방식과 옆으로 이동하며 탐색하는 방식이 있다. 두 방식 모두 한 번 방문한 노드는 재탐색하지 않아야 하므로 이를 구분할 수 있는 flag 가 필요하다.

Node 클래스에 visited 프로퍼티를 추가하자.

class Node {
  constructor(data) {
    this.data = data;
    this.adjacent = new Set();
    this.visited = false;
  }
  
  // ...
}

그리고 탐색 여부를 초기화하는 헬퍼 메소드 Graph 클레스에 구현하자.

initVisitedData() {
  this.#nodes.forEach(node => node.visited = false);
}

DFS (높이 우선 탐섹) - 스택으로 구현

높이 우선탐색의 경우 시작 노드로 부터 아래 방향으로 탐색하고, 최대 깊이까지 탐색이 완료되면 다음 노드로 이동한다. 시작 노드에서 부터 인접노드가 있으면 인접노드를 탐색, 해당 인접 노드에 인접노드가 있으면 다시 입접도느를 탐색하는 방식이다.

데이터를 넣고빼는 관점에서 살펴보면 이는 스택자료구조를 사용하여 구현할 수 있다. 스택 자료구조는 후입선출 자료구조로, 먼저 들어온 요소를 제일 먼저 탐색한다. 스택에 인접요소를 모두 넣고 가장 나중에 들어간 인접요소의 인접요소를 다시 스택에 추가한다.

스택을 활용한 DFS 를 구현해 보자.

DFSByStack(v, callback) {
    const stack = new Stack();
    const startNode = this.#nodes.get(v);
    startNode.visited = true;
    stack.push(startNode);
    
    while (!stack.isEmpty) {
      const currentNode = stack.pop();
      const adjacentList = currentNode.getAdjacent();
      adjacentList.forEach((a) => {
        const adjacentNode = this.#nodes.get(a);
        if (!adjacentNode.visited) {
          adjacentNode.visited = true;
          stack.push(adjacentNode);
        }
      });
    
      if (callback && typeof callback === 'function') {
        callback(currentNode);
      }
    }
}

스택에 탐색 대상을 넣어가며 가장 깊은 곳 까지 탐색하고, 스택이 비면 동작을 멈춘다.

DFS 를 테스트 해 보자.

graph.DFSByStack('A', ({ data }) => console.log(data));

테스트의 결과는 다음과 같다.

DFS (높이 우선 탐섹) - 재귀함수로 구현

높이 우선 탐색의 경우 인접 노드를 재귀적으로 탐색하는 방식으로 구현할 수도 있다.

DFSByRecursion(node, callback) {
    if (!node) return null;

    node.visited = true;
    if (callback && typeof callback === 'function') {
      callback(node);
    }

    const adjacentList = node.getAdjacent();
    adjacentList.forEach((a) => {
      const adjacentNode = this.#nodes.get(a);
      if (!adjacentNode.visited) {
        this.DFSByRecursion(adjacentNode, callback);
      }
    });
  }

노드를 인수로 받도록 작성되었다. 코드를 테스트 해 보자.

graph.DFSByRecursion(graph.getVertex('A'), ({ data }) => console.log(data));

테스트 결과는 다음과 같다.

같은 너비 탐색이지만 결과가 다른 이유는 스택이 후입선출이라는 점을 알고있다면 이해가 될 것이다. 스택을 활용한 DFS 같은 경우에는 후에 link 가 걸린 노드가 가장 나중에 스택에 추가되고 가장 먼저 스택에서 꺼내지기 때문에 그래프의 오른쪽부터 높이 우선 탐색을 한다.

BFS (너비 우선 탐색)

너비 우선 탐색은 그래프의 너비를 우선으로 탐색하는 탐색 알고리즘이다. 이는 자료 구조 중 큐를 사용하여 구현할 수 있다. 큐는 선입선출 자료 구조로, 인접 노드들을 큐에 추가하면 시작 노드의 인접노드를 모두 탐색하고 다음 노드로 이동한다.

코드를 통해 살펴보자.

BFSByQueue(v, callback) {
  const queue = new Queue();
  const startNode = this.#nodes.get(v);
  queue.enqueue(startNode);

  while (!queue.isEmpty) {
    const currentNode = queue.dequeue();
    const adjacentList = currentNode.getAdjacent();
    adjacentList.forEach((a) => {
      const adjacentNode = this.#nodes.get(a);
      if (!adjacentNode.visited) {
        adjacentNode.visited = true;
        queue.enqueue(adjacentNode);
      }
    });

    currentNode.visited = true;
    if (callback && typeof callback === 'function') {
      callback(currentNode);
    }
  }
}

큐가 비어있을 때 까지 반복하며, 노드에서 인접노드를 큐에 계속 추가하며 작업한다.

코드가 정상 동작하는지 테스트해 보자.

graph.BFSByQueue('A', ({ data }) => console.log(data));

테스트의 결과는 다음과 같다.

전체 코드는 링크에서 확인할 수 있다.

end

비선형 자료 구조인 그래프에 대해 알아보고, 스택, 큐를 사용하여 DFS, BFS 탐색 알고리즘을 구현해 보았다.